応力 vs ひずみ: 主な違いとその意味を理解する

応力とひずみは、特定の材料が外部からの圧力を受け入れる能力を測定する 2 つの関連用語です。. 応力とは、材料にかかる力の量です。. 一方で, 材料がその挙動を変えることを余儀なくされたとき, 緊張と呼ばれます. これらの力がどのように作用するかを理解することで、エンジニアは構造用の安全で効率的な材料を開発することが容易になります。. それで, この記事では、応力と緊張の基本をさらに探求し、実際のこれらの要因の重要性についての一般的なアイデアを読者に提供します。.

ストレスをどう定義しますか?

応力は、隣接する 2 つの粒子に作用する内部力の大きさを推定するために、材料の単位面積に作用する力です。. その公式について話すと, 応力は単位面積あたりの力です. 通常はパスカルで測定されます (パ) または平方メートルあたりのニュートン (N/㎡). その数学的表現は次のとおりです。:

σ=F/A

ここで、F は加えられる力、A はチャネルの断面積を表します。.

ストレスの重要性

応力とは主に、材料の領域に加えられる力を指します。. 材料に力を加えると内部力が発生します. さらに, これらの力は材料全体に広がります. 単位面積あたりに作用する力は、応力と呼ばれるもので表されます。. 応力を認識することは、材料が限界点に達することなくさまざまな荷重下でどのように動作するかを特定するのに役立ちます。.

さまざまな種類のストレス

その他のストレスについてはこちら

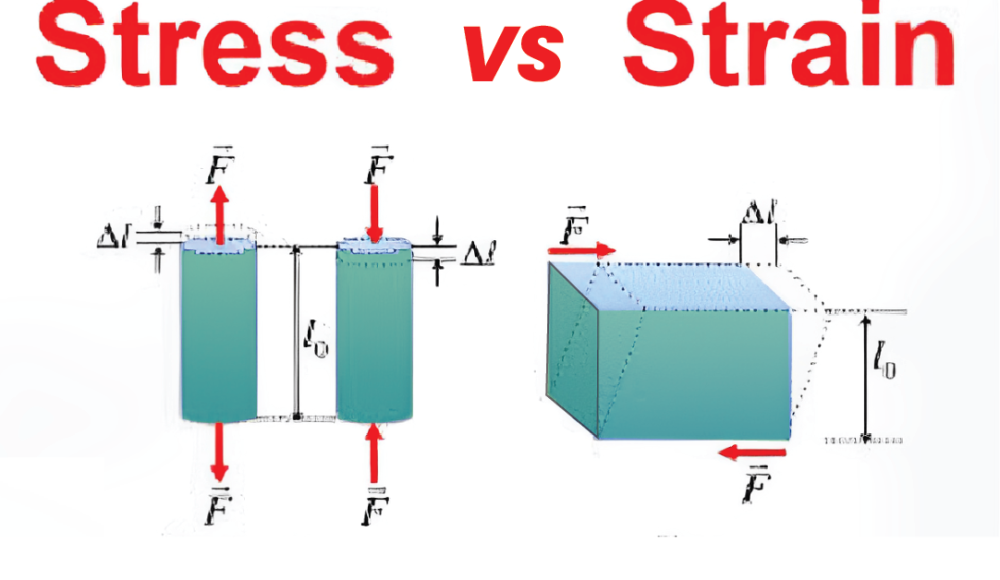
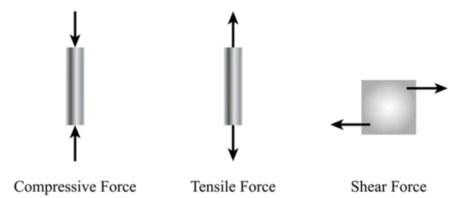
1. 引張応力: これは通常、応力によって材料が新しい平行長さに引っ張られるときに発生します。, つまり. 伸び. 例としては、輪ゴムの両端が離れてしまった場合です。.
2. 圧縮応力: 材料の特定の部分が互いに押し付けられると発生し、サイズが減少します。. 例えば. 弓とスプリングの圧縮を受けるために弓を曲げて低く曲げます.
3. せん断応力: 力が材料の特定の部分に平行な場合に発生します。. このほかにも, 材料の層が互いに滑ります。. 例としては、紙を切るときに使うハサミです。.
4. 曲げ応力: 一般的には変形によって起こります. それは次のときに発生します。 材料が曲がり始める 引張力と圧縮力の両方による荷重による. 例としては、梁の中央に荷重が加わった場合の梁のたわみがあります。.
5. ねじり応力: これは、材料のせん断応力につながるねじり荷重によって生じる直接的な応力です。. 例としては、両端にトルクをかけて回転する金属棒があります。.

ストレスの原因

ストレスの主な原因は以下の通りです;

1. 外力

あらゆる構造に​​作用する外部荷重は、材料に直接力を加え、応力を引き起こします。. これらの力は張力となる可能性があります, 圧縮, そして剪断します. 合力は狭い領域では非常に大きくなります. このほかにも, 動的応力は一定の振動圧力です. 通常、材料を徐々に摩耗させる疲労応力を引き起こす原因となります。.

2. 環境要因

熱は材料の寸法に影響を与え、サイズを拡大または縮小します。. このほかにも, 化学的攻撃により材料が弱くなり、内部応力が発生します。. 湿気や湿気は​​、特に吸湿性のあるものの膨張や劣化を引き起こします。. 振動は材料を機械的に変形させ、材料に応力を生じさせます。. さらに, 紫外線やガンマ線などの放射線, 物質に原子レベルのダメージを与える.

ストレスの測定方法?

ストレスを適切に測定する方法をいくつか紹介します。;

• ロードセル: 機械的な力を電気信号に変換するのに役立ちます。. このほかにも, さまざまなシナリオで正確かつ反復的な測定を行います。.
• ひずみゲージ: 電気抵抗の変化を分析することで変形を測定します. このほかにも, 内部応力を測定するための正確なひずみ測定を提供します。.

• 応力-ひずみ曲線: この曲線は、応力とひずみをプロットするのに役立ちます. 弾性および塑性の挙動を重要なポイントとともに明らかにします, つまり. 降伏点 (塑性変形開始), 極限引張強さ (最大応力), そして骨折点 (失敗). , さらに, この曲線は材料の選択や構造設計にも役立ちます.
• その他のテクニック: これらは視覚的ストレス パターンの光弾性となる可能性があります. このほかにも, 計算応力シミュレーション用の有限要素解析として使用できます。. さらに, これらの技術には、残留応力測定や音響放射のための X 線回折が含まれる場合があります。. それで, ストレス波を簡単に検出できる.

ひずみをどのように定義しますか?

ひずみとは、物質体内の粒子間の変位を表す変形の名前です。. この変位は基準長さを基準とすることができます. このほかにも, ひずみは、応力下で材料がどの程度変形するかを推定します。. その一般的な表現は、

ひずみ = 長さの変化 / 元の長さ. または

歪み (e) ϵ=ΔL/Lo

ひずみの重要性

ひずみは建設分野で非常に重要です. さまざまな荷重条件下で材料がどのように動作するかを予測するのに役立ちます. このほかにも, エンジニアは、荷重を取り除いた後に材料が元の形状に戻るかどうかを検討できます。 (弾性挙動). それで, このひずみは、工学用途において構造の完全性を確保し、材料の破損を防ぐための知識を得るのに役立ちます。.

ひずみの原因

以下の要因により、さまざまな材料にひずみが発生します。:

1. 外力

自己適用荷重, つまり. 張力, 圧縮, せん断力, 曲げ力, トルクは材料の変形を直接引き起こします. これらの力により材料の形状やサイズが変化し、ひずみが生じます。.

2. 環境要因

熱と寒さは材料のサイズに影響を与えるため、熱応力が発生します. 化学薬品によっては素材の変形や劣化を引き起こす可能性があるものもあります. このほかにも, 一部の材料の水分含有量が変化すると、材料は膨張または収縮します。. 放射線は材料内の格子に原子レベルで変化を引き起こし、その結果歪みが生じる可能性があります。.

ひずみの測定方法?

ひずみ測定技術について詳しく説明します;

1. ひずみゲージ: 特定の物質の歪みのレベルを定量化するために使用されるセンサーは、ひずみゲージとして知られています。. その過程で, しかし, 材料を変形させ、電気抵抗を変化させます。.
2. 伸び計: これらの装置は、材料サンプルに荷重が加えられたときの、材料サンプルの長さのゲージ変化を測定します。. これらは引張試験に幅広く応用できます.

3. デジタル画像相関 (DIC):これは、デジタル画像を使用して材料表面の歪みを観察する、わかりやすい光学優勢制御技術です。. 全磁場ひずみを測定可能. このほかにも, 詳細な情報が必要なひずみ解析に効率的です.
4. 光弾性: 偏光顕微鏡を用いてひずみを可視化するプロセスです. このほかにも, 偏光の原理を利用しています. これらは、高応力領域を特定し、困難なひずみパターンを理解するのに役立ちます。.
5. 有限要素解析 (FEA):さまざまな荷重が作用したときの材料の変形を予測する数値手法の 1 つです。. 特定の株情報を処理します. この情報は、材料とシステムの適切なフレームワークと設計を決定するのに役立ちます。.

応力とひずみの主な違い

応力とひずみの主な違いをよりよく理解するための表を次に示します。.

ストレス	歪み
材料内の単位面積当たりに作用する力として定義できます。.	元の長さに対する変形です
これは σ=F /A として表すことができます。	ϵ=ΔL/L0と表すことができます。
単位 = パスカル (パ) または平方メートルあたりのニュートン (N/㎡)	同じパラメータの比率なので無次元です
応力による内部力の推定値の取得	単にメジャーの形状やサイズが変化するだけです
外力や環境要因によって引き起こされる	外力や環境要因によって引き起こされる
種類: 引張, 圧縮性, 剪断, 曲げ, ねじれ	種類: 引張, 圧縮性, 剪断, 曲げ, ねじれ
材料の耐力を示します	力が加わったときの材料の変形を示します
ロードセルで測定, ひずみゲージ, 応力-ひずみ曲線, FEA	ひずみゲージで測定, 伸び計, DIC, FEA
材料の選択に使用されます, 構造設計, 故障予測	パフォーマンス分析で使用される, 変形の研究, 構造的完全性

ストレスと緊張はどのように関係するのか?

もともと応力とひずみは材料科学の分野で密接な関係にある概念です。. 応力は、材料が受ける単位面積当たりの力として定義されます。, 一方、ひずみは、応力を受けたときの材料の寸法の変化です。. 応力とひずみの相関関係は、通常、応力がかかったときの材料の挙動を示す応力-ひずみ図で表されます。. 弾性領域では, 応力とひずみは正比例し、フックの法則に支配されます。, つまり. σ=Eϵ

ストレスをどのように定義しますか 対 ひずみ曲線?

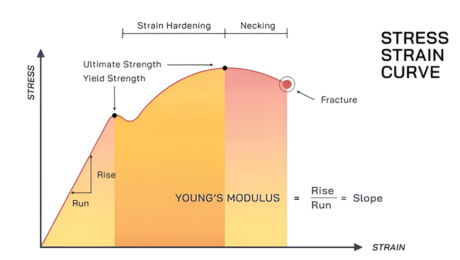
応力対ひずみ曲線 – 材料にかかる応力の量とそれが示すひずみの量をグラフで表現したもの. それで. 以下にその主要な領域と曲線上の点を示します。:

• 弾性領域: フックの法則で示されるように、応力とひずみの関係が正比例する領域; つまり. σ=Eϵ. ここ, 応力が除去された後、材料は元の形状に戻ります.
• 降伏点: 材料は降伏点を超えて曲がり始め、応力が解放されても永久変形が発生します。.
• プラスチック領域: この時点で, 材料は降伏段階を超えると永久に固まります.
• 極限引張強さ: 材料が特にネッキング点まで耐えることができる応力の量.
• 破壊点: 真の故障点とも呼ばれます, これは材料の破壊点の位置です.

曲線は材料の特性を説明するのにも不可欠です. このほかにも, エンジニアリング設計プロセスで適切な材料を選択するプロセスに役立ちます。.

結論

結論は, ストレスv. 歪み, 応力とひずみは材料科学と材料工学の基本概念です. さまざまな力から生じる物質の反応を学ぶ上で非常に価値があります。. 材料の内部力を定義する応力と同様, ひずみは力に伴う変形を定義します. 関係の種類を表す応力-ひずみ曲線は、材料の特性と挙動を一般的に理解する上で非常に価値があります。. したがって, エンジニアや科学者がこれらの概念を習得することで、より安全で効率的な構造と材料の開発が可能になります。. お問い合わせ 詳細については.